Complex Transform Calculator

Als je ooit complexe analyse hebt bestudeerd en met name complexe vlakke transformaties van de vorm w = f (z), dan kan deze toepassing interessant zijn.

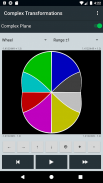
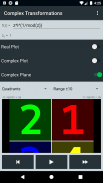
U kunt constanten en uitdrukkingen definiëren met behulp van een uitgebreide set wiskundige functies en vervolgens een transformatie toepassen op zowel een enkele waarde van z als op een raster van waarden op het complexe vlak. Hiermee kunt u het effect van uw transformatie op het complexe vlak visualiseren. U weet bijvoorbeeld dat een bepaalde transformatie roteert en het vlak schaalt, maar met deze toepassing kunt u het daadwerkelijk zien gebeuren. U kunt de transformatie een keer toepassen of, indien van toepassing, telkens opnieuw toepassen.

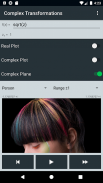
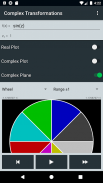
Echte en complexe plots bieden aanvullende visuele feedback wanneer u een transformatie toepast. De echte plot kan Re (z), Im (z), Mod (z) of Arg (z) weergeven. De complexe plot geeft waarden van z weer in een Argand-diagram. U kunt de echte plotmodus op elk moment wijzigen, zodat u duidelijk kunt zien hoe de waarden in de loop van de tijd veranderen. De plots maken deze applicatie een waardevol hulpmiddel voor het begrijpen van het effect dat een transformatie heeft op bepaalde waarden van z.

De krachtige complexe getal-expressie-evaluator betekent dat de toepassing ook kan worden gebruikt als een algemene, zij het enigszins onconventionele rekenmachine.

Alles wat u invoert op maximaal 10 werkbladen wordt automatisch opgeslagen terwijl u doorgaat, dus alles ziet er hetzelfde uit de volgende keer dat u de toepassing start. Dit betekent dat u tot 10 verschillende transformaties kunt definiëren en ze vervolgens kunt oproepen voor klassedemonstraties of discussies.

Ten slotte wordt u niet alleen gelaten om erachter te komen hoe de applicatie werkt. Er is een korte gebruikershandleiding, hulp bij uitdrukkingen en verschillende gedetailleerde voorbeelden die u kunt doornemen.

We hopen dat je het leuk vindt om deze applicatie te gebruiken en op zijn minst een beetje meer te leren over dit fascinerende gebied van de wiskunde.